Geometry Spot is a platform designed to make learning geometry more accessible and engaging. It combines interactive tools, educational resources, and practice exercises to help users of all ages understand and apply geometric concepts. The platform is aimed at students, teachers, and anyone interested in enhancing their geometry skills.
Geometry Games
Geometry games offer a fun and interactive way to engage with geometric concepts. They cater to various learning styles and can be a powerful tool that is used for better understanding. Here’s a closer look at different types of geometry games:
1. Shape Matching Games
Shape matching games help players recognize and associate geometric shapes with their names and properties. For instance, you might match a triangle with its attributes (e.g., three sides, the sum of interior angles is 180 degrees). These games enhance spatial awareness and shape recognition.
2. Geometry Puzzles
Geometry puzzles challenge players to solve problems or fit shapes into a given space. These puzzles can range from simple jigsaw puzzles to complex geometric problems that require critical thinking and spatial reasoning.
3. Virtual Geometry Tools
Virtual geometry tools provide interactive environments where users can draw, measure, and manipulate geometric shapes. These tools help visualize geometric concepts and explore properties in real-time.
4. Geometry Escape Rooms
Geometry escape rooms combine geometry with puzzle-solving in a fun, interactive format. Players solve a series of geometric problems to “escape” from a virtual room.
Geometry Quizzes
Quizzes are a great way to test your understanding and reinforce your knowledge of geometry. They come in various formats and cover different topics. Here’s a breakdown of common types of geometry quizzes:
1. Multiple Choice Questions
These quizzes present a question with several possible answers, only one of which is correct. They test your knowledge of geometric definitions, properties, and theorems.
Example Question: What is the sum of the interior angles of a triangle?
- A) 90 degrees
- B) 180 degrees
- C) 360 degrees
- D) 270 degrees
2. True or False Questions
True or false quizzes assess whether you can determine the validity of geometric statements. They are useful for understanding concepts and theorems.
Example Statement: The sum of the interior angles of a quadrilateral is 360 degrees. (True/False)
3. Fill-in-the-Blanks
Fill-in-the-blanks quizzes require you to complete sentences or equations with the correct geometric terms or values.
Example Question: The __________ of a circle is the distance around the circle. (Answer: circumference)
4. Problem Solving Quizzes
These quizzes present geometric problems that require applying various concepts and methods to find solutions.
Also Read: EzClasswork Guide
Pentagon, Octagon, Hexagon: Shapes Quizzes
Understanding different polygons and their properties is essential in geometry. Here’s how quizzes can help you learn about pentagons, hexagons, and octagons:
1. Pentagon Quizzes
Pentagons have five sides and five angles. Quizzes on pentagons might include:
- Identifying the number of sides and angles.
- Calculating the sum of interior angles.
- Distinguishing between regular and irregular pentagons.
2. Hexagon Quizzes
Hexagons have six sides and six angles. Quizzes may involve:
- Finding the area of regular hexagons.
- Understanding properties like symmetry and angle measures.
- Solving problems involving hexagonal tiling or patterns.
3. Octagon Quizzes
Octagons have eight sides and eight angles. Quizzes could focus on:
- Calculating the sum of interior angles.
- Identifying regular and irregular octagons.
- Solving problems related to octagonal patterns and designs.
Geometry Worksheets
Geometry worksheets are excellent tools for practicing and reinforcing your knowledge. They provide structured exercises and problems to help you apply geometric concepts. Here’s a breakdown of different types of geometry worksheets:
1. Basic Shape Worksheets
These worksheets focus on recognizing, drawing, and understanding basic geometric shapes like triangles, squares, and circles. They help build a solid foundation in geometry.
2. Angle Measurement Worksheets
These worksheets involve tasks such as measuring angles with a protractor, classifying types of angles, and solving problems related to angle properties.
3. Area and Perimeter Worksheets
Worksheets on area and perimeter help you practice calculating the area and perimeter of various shapes, including rectangles, triangles, and circles.
4. 3D Shapes Worksheets
These worksheets focus on understanding and calculating properties of 3D shapes such as cubes, spheres, and cylinders. They help visualize spatial relationships and volume calculations.
Understanding the Fundamentals
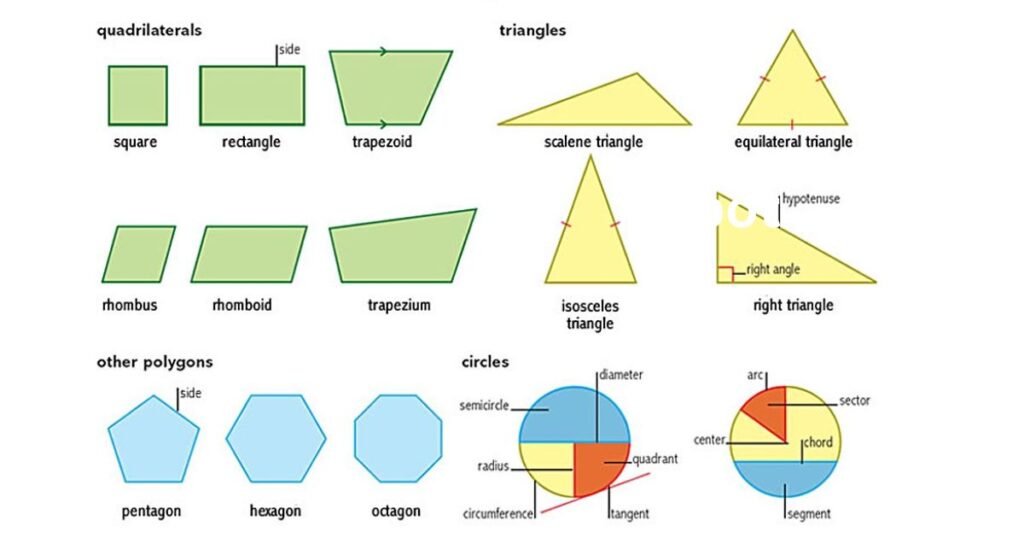
Mastering the basics is crucial for building a strong foundation in geometry. Here’s a closer look at fundamental concepts:
1. Shapes and Their Properties
Understanding shapes involves knowing their sides, angles, and other characteristics. Key shapes include:
- Triangles: Three sides, sum of angles is 180 degrees.
- Quadrilaterals: Four sides, sum of angles is 360 degrees.
- Circles: Defined by radius, diameter, and circumference.
2. Triangles
Triangles are classified based on their sides and angles:
- Equilateral: All sides and angles are equal.
- Isosceles: Two sides and two angles are equal.
- Scalene: All sides and angles are different.
Properties: The sum of the interior angles is always 180 degrees. The Pythagorean theorem applies to right-angled triangles.
3. Quadrilaterals
Quadrilaterals have four sides and can be further classified into:
- Squares: All sides and angles are equal, with each angle being 90 degrees.
- Rectangles: Opposite sides are equal, and each angle is 90 degrees.
- Parallelograms: Opposite sides are equal, and opposite angles are equal.
- Trapezoids: At least one pair of parallel sides.
4. Circles
Circles are defined by their center and radius. Key concepts include:
- Circumference: The distance around the circle.
- Area: The space enclosed by the circle.
- Diameter: The distance across the circle through its center.
5. Polygons
Polygons are multi-sided shapes. Important properties include:
- Sum of Interior Angles: (n−2)×180(n-2) \times 180(n−2)×180 degrees, where nnn is the number of sides.
- Regular Polygons: All sides and angles are equal.
6. 3D Shapes
3D shapes include:
- Cubes: All sides are equal, with 6 faces.
- Spheres: Perfectly round, with no edges or vertices.
- Cylinders: Two circular bases and a curved surface.
The Importance of Angles
Angles play a crucial role in geometry, helping define shapes and solve problems. Here’s why angles are significant:
1. Defining Shapes
Angles help determine the shape and properties of geometric figures. For example, the type of triangle is determined by its angles.
2. Problem Solving
Understanding angles is essential for solving geometric problems. Problems involving triangles, polygons, and circles often require angle calculations.
3. Real-Life Applications
Angles are used in various fields, such as:
- Architecture: Designing structures with precise angles for stability.
- Engineering: Creating mechanical parts that fit together accurately.
- Art: Creating geometric designs and patterns.
Geometry Around Us
Geometry is everywhere, from the design of everyday objects to the layout of buildings. Here’s how geometry appears in the world around us:
1. Architecture and Engineering
Geometric principles are crucial in designing buildings, bridges, and other structures. Architects use geometry to create aesthetically pleasing and functional designs.
2. Technology
Geometry is used in technology, such as computer graphics and virtual reality. Geometric algorithms help create realistic images and animations.
3. Nature
Nature is full of geometric patterns and shapes. Examples include the hexagonal structure of honeycombs and the symmetry of flowers.
4. Art and Design
Artists use geometric shapes and patterns to create visual harmony in their works. Geometric principles help in designing logos, patterns, and artwork.
Tips for Mastering Geometry
To excel in geometry, follow these tips:
1. Grasp the Basics Firmly
Start with a solid understanding of basic concepts and terminology. Ensure you are comfortable with shapes, angles, and their properties.
2. Visual Learning
Use visual aids like diagrams and drawings to understand geometric concepts. Visualizing problems can help you grasp complex ideas more easily.
3. Practice Regularly
Regular practice is essential for mastering geometry. Solve various problems and exercises to reinforce your understanding and improve your skills.
4. Learn Theorems and Formulas
Familiarize yourself with important theorems and formulas. Understanding these will help you solve problems more efficiently and effectively.
5. Use Technology
Leverage technology, such as geometry software and online tools, to explore geometric concepts and visualize problems.
6. Engage in Proof Writing
Writing geometric proofs helps deepen your understanding and develop logical reasoning skills. Practice proving theorems and solving problems step-by-step.
7. Connect Geometry with Real Life
Relate geometric concepts to real-life situations to make learning more relevant and interesting. For example, think about how geometry applies to architecture or art.
8. Collaborate and Discuss
Work with others to solve problems and discuss geometric concepts. Collaboration can provide new insights and enhance your understanding.
9. Seek Help When Needed
Don’t hesitate to ask for help if you’re struggling with a concept. Seek assistance from teachers, tutors, or online resources.
10. Stay Curious and Explore
Keep exploring new geometric concepts and applications. Stay curious and continue learning to expand your knowledge and skills.
Exploring Non-Euclidean Geometry
Non-Euclidean geometry extends beyond the traditional Euclidean principles and explores different spatial relationships. Here’s an overview of non-Euclidean geometry:
1. What is Non-Euclidean Geometry?
Non-Euclidean geometry studies geometries that are not based on Euclid’s parallel postulate. It includes:
- Hyperbolic Geometry: Involves a space where the parallel postulate does not hold. Lines diverge, and angles in triangles sum to less than 180 degrees.
- Elliptic Geometry: Involves a space where no parallel lines exist. All lines eventually intersect, and angles in triangles sum to more than 180 degrees.
2. Implications and Applications
Non-Euclidean geometry has significant implications in various fields:
- Physics: The theory of relativity uses non-Euclidean geometry to describe the curvature of space-time.
- Art: Artists use non-Euclidean concepts to create unique visual representations of space.
- Astronomy: Understanding the shape of the universe involves non-Euclidean geometry.
3. Understanding and Visualization
Visualizing non-Euclidean spaces can be challenging. Using models, simulations, and interactive tools can help in understanding these complex geometries.
4. Challenges and Opportunities
Non-Euclidean geometry presents challenges in visualization and application. However, it also offers opportunities for innovation and exploration in various scientific and artistic fields.
What Makes Geometry Spot Unique?
Geometry Spot is an exceptional platform for geometry enthusiasts and learners. Here’s what sets it apart:
1. Interactive Tools
Geometry Spot provides interactive tools that allow users to visualize and manipulate geometric shapes. These tools help in understanding concepts and solving problems.
2. Educational Resources
The platform offers a wealth of educational resources, including tutorials, videos, and worksheets. These resources support various learning styles and levels.
3. Practice Exercises
Geometry Spot includes numerous practice exercises and quizzes to reinforce learning and track progress. These exercises cover a wide range of topics and difficulty levels.
4. Customizable Learning
The platform caters to different learning preferences by offering customizable learning experiences. Users can choose resources and exercises that match their needs and goals.
Conclusion
Geometry involves engaging with interactive games, quizzes, and worksheets that make learning both fun and effective. By understanding fundamental concepts such as shapes, angles, and polygons, and exploring advanced topics like non-Euclidean geometry, learners can develop a deep appreciation for this field. Geometry Spot stands out as a valuable resource by offering interactive tools, comprehensive educational materials, and customizable learning experiences that cater to diverse needs. Embracing these resources and strategies not only enhances your geometric skills but also connects you with the real-world applications of this fascinating discipline.
Frequently Asked Questions
What is Geometry Spot?
Geometry Spot is an online platform that provides interactive tools, educational resources, and practice exercises to help users learn and master geometry.
How can I use Geometry Spot to improve my geometry skills?
You can use Geometry Spot’s interactive tools to visualize geometric concepts, practice problems with various exercises, and access educational resources to deepen your understanding.
What are some effective strategies for learning geometry?
Effective strategies include grasping the basics firmly, using visual aids, practicing regularly, learning theorems and formulas, and connecting geometry with real-life situations.
What is non-Euclidean geometry?
Non-Euclidean geometry explores geometries that differ from Euclidean principles, involving curved spaces and providing new perspectives on spatial relationships.
How can non-Euclidean geometry be applied in real life?
Non-Euclidean geometry has applications in fields such as physics, art, and architecture, offering new ways to understand and represent space.
What makes Geometry Spot different from other geometry learning platforms?
Geometry Spot is unique for its interactive tools, comprehensive educational resources, customizable learning experiences, and focus on both fundamental and advanced geometric concepts.